Lettis.Net

The statistical analysis of molecular dynamics simulations requires dimensionality reduction techniques, which yield a low-dimensional set of collective variables (CVs) {xi} = x that in some sense describe the essential dynamics of the system. Considering the distribution P(x) of the CVs, the primal goal of a statistical analysis is to detect the characteristic features of P(x), in particular, its maxima and their connection paths. This is because these features characterize the low-energy regions and the energy barriers of the corresponding free energy landscape ΔG(x) = −kBT ln P(x), and therefore amount to the metastable states and transition regions of the system. In this perspective, we outline a systematic strategy to identify CVs and metastable states, which subsequently can be employed to construct a Langevin or a Markov state model of the dynamics. In particular, we account for the still limited sampling typically achieved by molecular dynamics simulations, which in practice seriously limits the applicability of theories (e.g., assuming ergodicity) and black-box software tools (e.g., using redundant input coordinates). We show that it is essential to use internal (rather than Cartesian) input coordinates, employ dimensionality reduction methods that avoid rescaling errors (such as principal component analysis), and perform density based (rather than k-means-type) clustering. Finally, we briefly discuss a machine learning approach to dimensionality reduction, which highlights the essential internal coordinates of a system and may reveal hidden reaction mechanisms.

The molecular actions of proteins occur along reaction coordinates. Current computer methods have limited ability to explore them. We describe a fast protocol called MELD-path that (1) efficiently samples relevant conformational states via MELD, an accelerator of Molecular Dynamics (MD), (2) seeds multiple short MD trajectories from MELD states, and then (3) constructs Markov State Models (MSM) that give the routes and kinetics. We tested the method against extensive (multi μs) MD simulations of the right-handed- to left-handed-helix transition of a 9-mer peptide of AIB, the symmetry of which allows us to establish convergence. MELD-path finds all the metastable states, their correct relative populations, and the full ensemble of routes, not just a single assumed route. For this transition, we find a very broad route structure. MELD-path is highly parallelizable and efficient, yielding the full route map in a few days of computation. We believe MELD-path could be a general and rapid way to explore mechanistic processes in biomolecules on the computer.

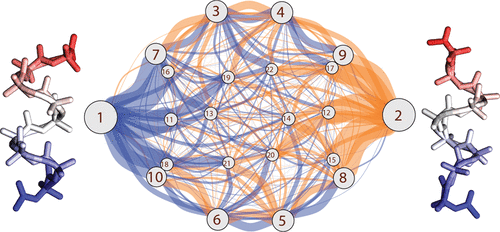
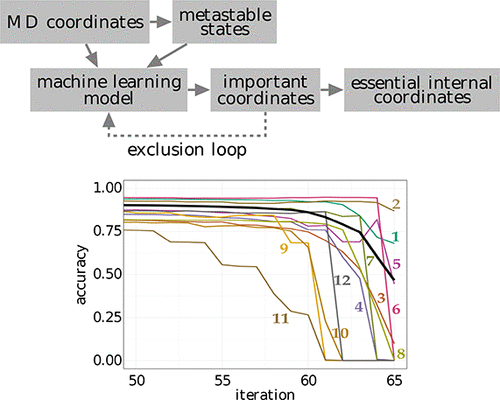We present a systematic approach to reduce the dimensionality of a complex molecular system. Starting with a data set of molecular coordinates (obtained from experiment or simulation) and an associated set of metastable conformational states (obtained from clustering the data), a supervised machine learning model is trained to assign unknown molecular structures to the set of metastable states. In this way, the model learns to determine the features of the molecular coordinates that are most important to discriminate the states. Using a new algorithm that exploits this feature importance via an iterative exclusion principle, we identify the essential internal coordinates (such as specific interatomic distances or dihedral angles) of the system, which are shown to represent versatile reaction coordinates that account for the dynamics of the slow degrees of freedom and explain the mechanism of the underlying processes. Moreover, these coordinates give rise to a free energy landscape that may reveal previously hidden intermediate states of the system.

A dimensionality reduction method for high-dimensional circular data is developed, which is based on a principal component analysis (PCA) of data points on a torus. Adopting a geometrical view of PCA, various distance measures on a torus are introduced and the associated problem of projecting data onto the principal subspaces is discussed. The main idea is that the (periodicity-induced) projection error can be minimized by transforming the data such that the maximal gap of the sampling is shifted to the periodic boundary. In a second step, the covariance matrix and its eigendecomposition can be computed in a standard manner. Adopting molecular dynamics simulations of two well-established biomolecular systems (Aib9 and villin headpiece), the potential of the method to analyze the dynamics of backbone dihedral angles is demonstrated. The new approach allows for a robust and well-defined construction of metastable states and provides low-dimensional reaction coordinates that accurately describe the free energy landscape. Moreover, it offers a direct interpretation of covariances and principal components in terms of the angular variables. Apart from its application to PCA, the method of maximal gap shifting is general and can be applied to any other dimensionality reduction method for circular data.

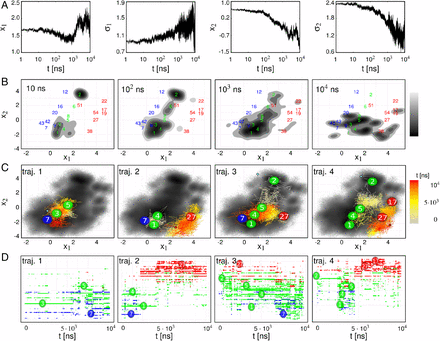Allostery represents a fundamental mechanism of biological regulation that is mediated via long-range communication between distant protein sites. Although little is known about the underlying dynamical process, recent time-resolved infrared spectroscopy experiments on a photoswitchable PDZ domain (PDZ2S) have indicated that the allosteric transition occurs on multiple timescales. Here, using extensive nonequilibrium molecular dynamics simulations, a time-dependent picture of the allosteric communication in PDZ2S is developed. The simulations reveal that allostery amounts to the propagation of structural and dynamical changes that are genuinely nonlinear and can occur in a nonlocal fashion. A dynamic network model is constructed that illustrates the hierarchy and exceeding structural heterogeneity of the process. In compelling agreement with experiment, three physically distinct phases of the time evolution are identified, describing elastic response (≲0.1 ns), inelastic reorganization (∼100 ns), and structural relaxation (≳1μs). Issues such as the similarity to downhill folding as well as the interpretation of allosteric pathways are discussed.

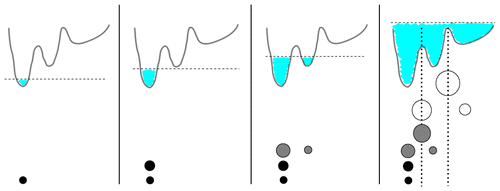A density-based clustering method is proposed that is deterministic, computationally efficient, and self-consistent in its parameter choice. By calculating a geometric coordinate space density for every point of a given data set, a local free energy is defined. On the basis of these free energy estimates, the frames are lumped into local free energy minima, ultimately forming microstates separated by local free energy barriers. The algorithm is embedded into a complete workflow to robustly generate Markov state models from molecular dynamics trajectories. It consists of (i) preprocessing of the data via principal component analysis in order to reduce the dimensionality of the problem, (ii) proposed density-based clustering to generate microstates, and (iii) dynamical clustering via the most probable path algorithm to construct metastable states. To characterize the resulting state-resolved conformational distribution, dihedral angle content color plots are introduced which identify structural differences of protein states in a concise way. To illustrate the performance of the method, three well-established model problems are adopted: conformational transitions of hepta-alanine, folding of villin headpiece, and functional dynamics of bovine pancreatic trypsin inhibitor.

To interpret molecular dynamics simulations of complex systems, systematic dimensionality reduction methods such as principal component analysis (PCA) represent a well-established and popular approach. Apart from Cartesian coordinates, internal coordinates, e.g., backbone dihedral angles or various kinds of distances, may be used as input data in a PCA. Adopting two well-known model problems, folding of villin headpiece and the functional dynamics of BPTI, a systematic study of PCA using distance-based measures is presented which employs distances between Cα-atoms as well as distances between inter-residue contacts including side chains. While this approach seems prohibitive for larger systems due to the quadratic scaling of the number of distances with the size of the molecule, it is shown that it is sufficient (and sometimes even better) to include only relatively few selected distances in the analysis. The quality of the PCA is assessed by considering the resolution of the resulting free energy landscape (to identify metastable conformational states and barriers) and the decay behavior of the corresponding autocorrelation functions (to test the time scale separation of the PCA). By comparing results obtained with distance-based, dihedral angle, and Cartesian coordinates, the study shows that the choice of input variables may drastically influence the outcome of a PCA.

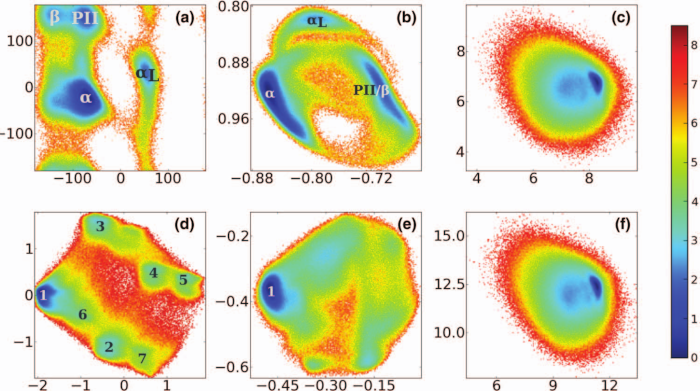Principal component analysis of molecular dynamics simulations is a popular method to account for the essential dynamics of the system on a low-dimensional free energy landscape. Using Cartesian coordinates, first the translation and overall rotation need to be removed from the trajectory. Since the rotation depends via the moment of inertia on the molecule's structure, this separation is only straightforward for relatively rigid systems. Adopting millisecond molecular dynamics simulations of the folding of villin headpiece and the functional dynamics of BPTI provided by D. E. Shaw Research, it is demonstrated via a comparison of local and global rotational fitting that the structural dynamics of flexible molecules necessarily results in a mixing of overall and internal motion. Even for the small-amplitude functional motion of BPTI, the conformational distribution obtained from a Cartesian principal component analysis therefore reflects to some extend the dominant overall motion rather than the much smaller internal motion of the protein. Internal coordinates such as backbone dihedral angles, on the other hand, are found to yield correct and well-resolved energy landscapes for both examples. The virtues and shortcomings of the choice of various fitting schemes and coordinate sets as well as the generality of these results are discussed in some detail.

In recent years, small flying robots have become a popular platform in robotics due to their low cost and versatile use. In the context of autonomous navigation, low-cost robots are often equipped with imprecise sensors and actuators and require a proper calibration and carefully designed and learned models. External systems like motion capture cameras usually provide accurate pose estimates for such devices. However, they do not provide the translational and rotational velocities and accelerations of the object. In this paper, we present an algorithm for accurate calculations of the six-dimensional velocity and the six-dimensional acceleration from a possibly noisy pose time sequence. We compute the velocities and accelerations in a regression using Newton's equation of motion as the model function. Thereby, we efficiently decouple the six individual dimensions and account for fictitious forces in the non-inertial body-fixed frame of reference. In simulation and experiments with a real inertial measurement unit (IMU), we show that our algorithm provides accurate velocity and acceleration estimates compared to the reference data.